CPSC 330 Lecture 16: DBSCAN, Hierarchical Clustering

Happy Halloween

Announcements

  • HW5 extension: Was due yesterday
  • HW6 is due next week Wednesday.
    • Computationally intensive
    • You need to install many packages

Imports

iClicker Exercise 16.1

Select all of the following statements which are TRUE.

    1. Similar to K-nearest neighbours, K-Means is a non parametric model.
    1. The meaning of K in K-nearest neighbours and K-Means clustering is very similar.
    1. Scaling of input features is crucial in clustering.
    1. In clustering, it’s almost always a good idea to find equal-sized clusters.

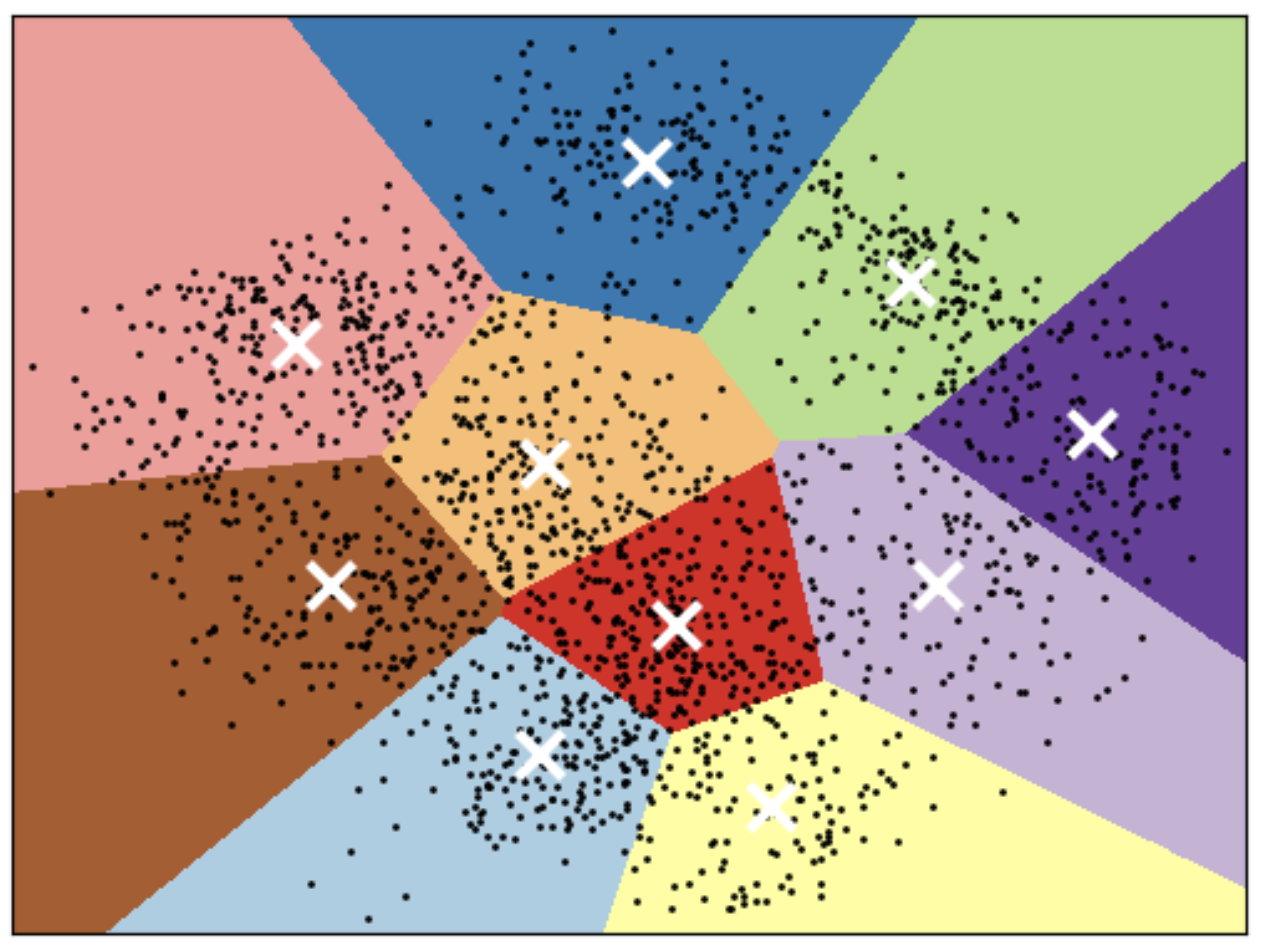
K-means Limitations

Shape of clusters

  • Good for spherical clusters of more or less equal sizes

K-Means: failure case 1

  • K-Means performs poorly if the clusters have more complex shapes (e.g., two moons data below).

K-Means: failure case 2

  • Again, K-Means is unable to capture complex cluster shapes.

K-Means: failure case 3

  • It assumes that all directions are equally important for each cluster and fails to identify non-spherical clusters.

Can we do better?

DBSCAN

  • Density-Based Spatial Clustering of Applications with Noise
  • A density-based clustering algorithm
X, y = make_moons(n_samples=200, noise=0.08, random_state=42)
dbscan = DBSCAN(eps=0.2)
dbscan.fit(X)
plot_original_clustered(X, dbscan, dbscan.labels_)

How does it work?

DBSCAN Analogy

Consider DBSCAN in a social context:

  • Social butterflies (🦋): Core points
  • Friends of social butterflies who are not social butterflies: Border points
  • Lone wolves (🐺): Noise points

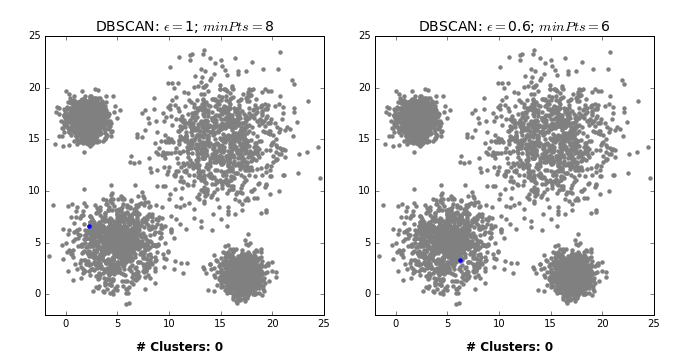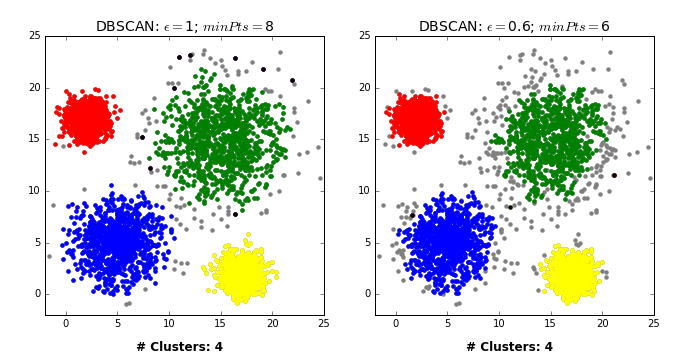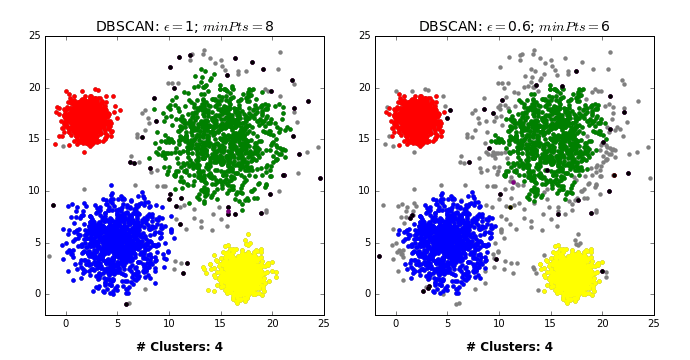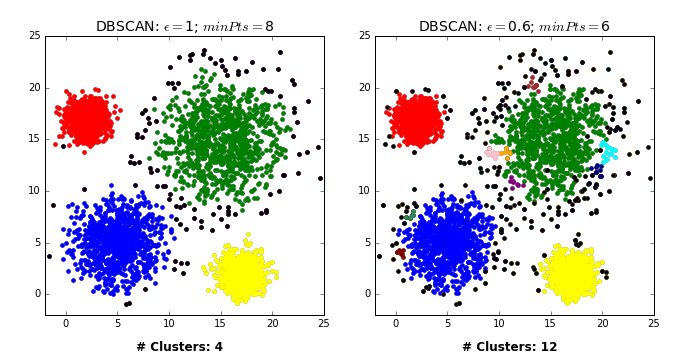
Two main hyperparameters

  • eps: determines what it means for points to be “close”
  • min_samples: determines the number of neighboring points we require to consider in order for a point to be part of a cluster

DBSCAN: failure cases

  • Let’s consider this dataset with three clusters of varying densities.
  • K-Means performs better compared to DBSCAN. But it has the benefit of knowing the value of K in advance.
[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15]

Hierarchical clustering

Dendrogram

  • Dendrogram is a tree-like plot.
  • On the x-axis we have data points.
  • On the y-axis we have distances between clusters.

Flat clusters

  • This is good but how can we get cluster labels from a dendrogram?
  • We can bring the clustering to a “flat” format use fcluster

Flat clusters

from scipy.cluster.hierarchy import fcluster
# flattening the dendrogram based on maximum number of clusters. 
hier_labels1 = fcluster(linkage_array, 3, criterion="maxclust") 
plot_dendrogram_clusters(X, linkage_array, hier_labels1, title="flattened with max_clusts=3")

Linkage criteria

  • When we create a dendrogram, we need to calculate distance between clusters. How do we measure distances between clusters?
  • The linkage criteria determines how to find similarity between clusters:
  • Some example linkage criteria are:
    • Single linkage → smallest minimal distance, leads to loose clusters
    • Complete linkage → smallest maximum distance, leads to tight clusters
    • Average linkage → smallest average distance between all pairs of points in the clusters
    • Ward linkage → smallest increase in within-cluster variance, leads to equally sized clusters

Activity

  • Fill in the table below in this Google doc: https://shorturl.at/3yOdg
Clustering Method KMeans DBSCAN Hierarchical Clustering
Approach
Hyperparameters
Shape of clusters
Handling noise
Examples

Class demo